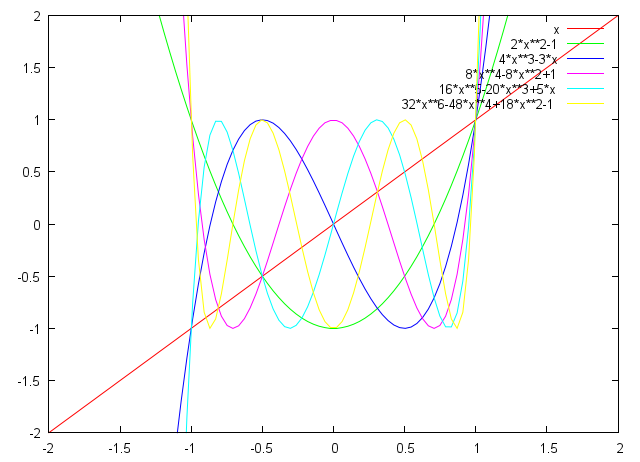
Definujeme si jednoduchú rekurentnú reláciu pre polynómy. Nič svetuborné.
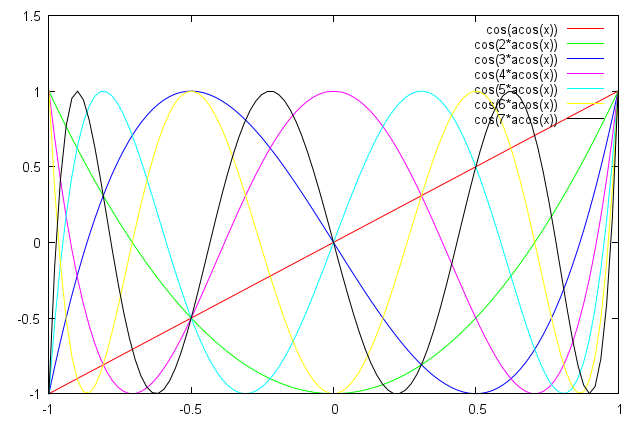
Potom si povieme, že je to vlastne rekurentná relácia s parametrom x. Riešením jej charakteristického polynómu sú pre |x|<1 komplexné čísla. Navyše to vychádza tak pekne, že vieme substituovať cos(fi) za x a máme rovno goniometrický tvar komplexného čísla.
Pridaním začiatočných podmienok sme dostali jednoznačné riešenie a spätnou substitúciou vzťah
T_n(x) = cos(n*arccos(x)) pre |x|<1. Tým sme určili nekonečne veľa bodov polynómu a teda existuje práve jeden taký polynóm (hodnoty extrapolujeme).
Keď som si to celé uvedomil, tak som bol proste ohúrený :). Viac informácií na wiki. Prikladám aj grafy vytvorené programom GNUplot. Učivo pochádza z Numerickej matematiky, teoretický blok informatiky, bakalársky stupeň, 3. ročník.
Normalizované Čebyševové polynómy
One thought on “Čebyševové polynómy”